[00:31.593]愛した数だけの 別れと涙が
[00:31.593]伴随着爱的离别与泪水
[00:37.886]僕らを優しく 包み込む
[00:37.886]温柔地将我们紧紧包围着
[00:43.995]そんな日は いつも同じように
[00:43.995]这样的日子从未改变
[00:54.732]胸の中に残る 僅かな希望を
[00:54.732]心中尚存的一丝希望
[01:00.752]求め続けてる
[01:00.752]仍在不断追寻着
[01:05.069]分かってた 君のこと
[01:05.069]已然知晓的你
[01:10.925]失いたくないと
[01:10.925]我不想失去
[01:16.902]また通り過ぎてく
[01:16.902]一如既往地共同度过
[01:20.862]時間だけが 二つの影
[01:20.862]相同的时间的话
[01:28.209]ひとつにして くれる筈と
[01:28.209]二人的影子就会融为一体
[01:33.938]信じたのに
[01:33.938]明明如此相信着
[01:39.550]あの空がもう一度 微笑んでくれたなら
[01:39.550]如果那片天空再一次对我露出微笑的话
[01:46.050]きっと 歩いてゆける
[01:46.050]就一定能够继续前行了吧
[01:51.184]永遠の孤独に立ち尽くす僕の心
[01:51.184]被永恒的孤独包围着的我的心
[01:59.828]つかまえて
[01:59.828]将它抓在手中
[02:02.988]このまま降り注ぐ 雨の中で流す涙に
[02:02.988]在滂沱泼洒的雨中哭泣着
[02:10.909]僕は誓うよ
[02:10.909]我发誓
[02:14.485]君のこと決して忘れはしないから
[02:14.485]绝对不会忘掉你
[02:20.671]ずっと 僕の中にいて
[02:20.671]将你永远深深藏在心中
[02:50.374]寄り添い手をつなぎ ふざけあっていた
[02:50.374]牵着手依偎在一起说笑着
[02:56.539]僕らはいつでも
[02:56.539]一直以来我们都是这样
[03:00.756]そんな日が繰り返し 続くと思っていた
[03:00.756]以为那样的日子今后也会重复下去
[03:12.441]まだ鮮明なまま
[03:12.441]生动的情景仿佛还在眼前
[03:16.467]色褪せずに 残る笑顔
[03:16.467]永不褪色的笑容
[03:23.795]愛おしくて 切なくなる
[03:23.795]因为爱而变得苦闷的
[03:29.672]この気持ちは
[03:29.672]这份心情
[03:35.152]永遠に変わらない だから僕は
[03:35.152]永远不会改变 所以我会
[03:39.912]前に向かって 歩いてゆける
[03:39.912]向前迈步
[03:47.044]大切なものを無くした痛みを抱えて
[03:47.044]怀着失去重要之物的痛苦
[03:55.556]今はただ
[03:55.556]如今只剩下
[03:58.623]手にしたぬくもりが君と僕を繋いでくれる
[03:58.623]残留在手中的余温将你我连结在一起
[04:06.590]だからもう一度
[04:06.590]因此再一次祈愿
[04:10.192]この空に願い届くまで祈りをこめて
[04:10.192]直到我的祈求传达到这片天空为止
[04:18.804]歌い続けるよ
[04:18.804]我会不断歌唱下去
[04:24.744]過ぎてゆく時間 何度でも
[04:24.744]流逝的时间 无论多少次
[04:33.212]季節をこの胸の中で巻き戻す
[04:33.212]都会在我的心中回溯
[04:47.488]あの空がもう一度 微笑んでくれたなら
[04:47.488]如果那片天空再一次对我露出微笑的话
[04:54.080]きっと 歩いてゆける
[04:54.080]就一定能够继续前行了吧
[04:59.398]永遠の孤独に立ち尽くす僕の心
[04:59.398]被永恒的孤独包围着的我的心
[05:07.956]つかまえて
[05:07.956]将它抓在手中
[05:10.952]このまま降り注ぐ 雨の中で流す涙に
[05:10.952]在滂沱泼洒的雨中哭泣着
[05:18.908]僕は誓うよ
[05:18.908]我发誓
[05:22.516]君のこと決して忘れはしないから
[05:22.516]绝对不会忘掉你
[05:28.751]ずっと 僕の中にいて
[05:28.751]将你永远深深藏在心中

吃喝玩乐，但也勿忘初心，路可以慢慢走，但不可以止步不前。

直至魔女消逝，我已经很久没有看过一个从OP到内容到ED，都让我身心如此宁静的动漫了，它可能比较冷门，亦或许比较平凡，但我一定要说道两句。开玩笑的，只能说鉴赏这种东西，我以前没做过，现在也不会做，以后也没有做的计划，但是由于我的人生越过越平凡了，能说的东西已经越来越少了，但又抑制不住自己想说话的欲望，所以有时候整点固定项目也挺好的，因为我也不想忘记那种码字的感觉。打分什么的就算了，以后就单纯地以我自己的主观感受评几个之最吧（有时候想要一个作品的时候，甚至可以强开一个分类，=^_^=）。

  • 综合：ある魔女が死ぬまで（伟大，无需多言）

  • 纯爱：男女の友情は成立する？（いや、 しないっ!!）（嗯哼，可惜Robot不是我的菜）

  • 日常：日々は過ぎれど飯うまし（虽说强行做饭，但吃饭乃人生大事）

  • 乐队：前橋ウィッチーズ（粉毛迷妹不是主角团，所以我选择另一个粉毛）

  • 女性：完璧すぎて可愛げがないと婚約破棄された聖女は隣国に売られる（虽说典中典中典，但是季度必填项目）

  • 异世界：最强の王样、二度目の人生は何をする？（季度必填爽文）

说起动漫，这个月我补了一个叫《欢迎加入NHK》的远古动漫，之所以会去看这部动漫是被别人的肥仔最后幻想的片段给吸引了，之所以会去补这个二十多集的长番是希望看到肥仔成就的那一刻，但当我发现那只不过是基友提醒男主产生的幻想时，我或许失望了一些，但投入的沉默成本让我看完了它。要我说怎么评价，只能说画面太老，前半季的ed过于魔性，甚至后半段还搞起来什么教育意义，比如有一个搞传销姐姐并沉迷于网游的大哥在一家餐饮店重生，又或者男主因家里断粮而被迫出去打工之类的。虽说它带来不了什么，但好歹给了我一段不错的体验，只要富有正能量，管他是什么先抑后扬的手法都是无所谓的。
说到教育意义，那就不得不谈前几天有些热门的《情感反诈模拟器》(《捞女游戏》)。我觉得改名是应该的，一方面是原名的针对性太强有一定的攻击性，另一方面则是，游戏本身其实是渣男捞女互斗，站在旁观者的角度上，实际上是用于告诫男女双方的。但我并不觉得它具有什么现实的教育意义，因为诈骗的成长是永无止境的，当你发觉的时候，它早就已经过时了。其更重要的警示作用，警示人们提高自己明辨是非的能力，对待诈骗要如同对待技术一般，存在敬畏之心，时刻保持害怕被骗的心理，虽然多疑一点会失去一些真诚，但至少可以减少被骗的概率，因为人都是现实的。虽然有人说，这只不过是“渣男操作捞女去搞龟男”的常规伎俩，但我觉得30元是值得的，从看完一部电影的角度来说，不管它是否有批判现实之嫌，但至少给予看过人了一些改变，我和大多数人的看法一样，前三章组成一部完整的电影佳作，加上后面几章的后宫爽文，剧情党和娱乐党都得到了满足。虽然我一直对真人电影不是很感冒，比如较久以前的那个“完蛋美女”，我就真没时间去玩，甚至都没买，也就B站稍微看了一点录播，但电影确实有些动漫做不到的事，就是演员的演技。为什么我一直对推子的演技不是很感冒？追它的原因也只是那个画师的画风让我有些喜欢(“人渣的本愿”是我以前初中就看过的经典代表)，就二次元那种画风而言，人物表情其实已经可以做得很丰富了，但如果说它是演的，我就不太信了，我只会觉得它本就是这样。
从现实回到二次元吧，最近的国g掀起了一点小波澜，其实我一直都是挺支持国g的，甚至steam里除了国g，就没有过日g。切割galgame属性其实没啥，叫视觉小说也就得了；负能量的传播，还是自己看看就算了；乱七八槽而又疯癫的剧情，我还是有那么点喜欢；卷钱跑路的话，确实过分的有些离谱了。嗯哼，其实我也在做g，但因为一个人又有工作，所以进度十分的缓慢，至于找人我的小金库还是差了不止一点的意思，趣味相投也不是那么好找的，所以一切的一切都只是妥协罢了。在我的目标里，至少有不切割galgame属性、爽文和正能量这几条，我就算心存幻想也不可能以什么大作作为目标，一个人单挑别人的团队，多少有些不现实，所以实打实地搞自己的精品小作，多多少少也能完成自己未了的遗愿，而且为了完成跨平台测试，我连mac和iphone都买了，就说我的决心够不够吗？我都不知道为什么，我还在追《欢迎来的实力至上主义教室》。嗯，原来路哥踢掉坂柳有栖是为了谋权篡位啊！妙哉，妙哉！说实话，除了几个主要角色，里面很多人我基本都没什么印象了，我不知什么时候说过，追更确实太难熬了，不如直接看完结作或galgame，要么就是收藏起来，养肥了再一次性看完。
说到玩galgame，不得不提一下我前些日子淘的洋垃圾

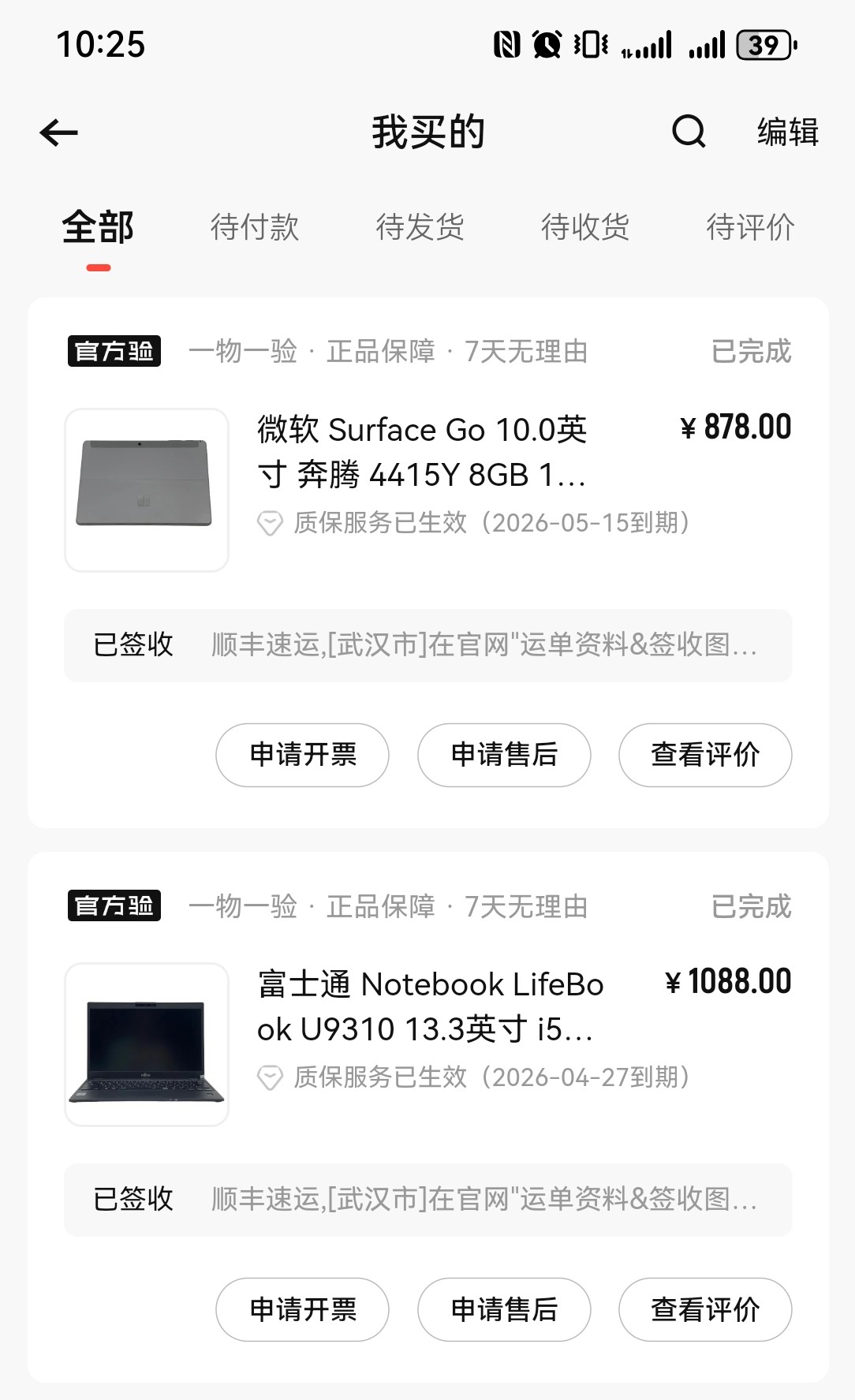
一台富士通和一台SurfaceGo，前者是因为我想要一个轻巧的办公本，用来方便携带的，当前市场里比富士通还轻的笔记本还是挺难找的，当然阉割电池我并不是很在意，因为我所处的工作环境基本哪里都有电源，但麻烦的就是要带来带去，所以我完全是按需选择的，而且用了两个多月，我觉得挺好的。至于SurfaceGo确实是个坑，其实我的需求挺简单的，就是床上玩galgame，所以选了x86架构的win平板，但是问题还挺多的，一是存档的同步，不用多说好吧，二是重量，虽说选了最轻的版本，但感觉还是不够，三是最让我绷不住的，有些galgame竟然还要双击才能到下一句对话。反正最后净亏三百多给出掉了，这其实挺让我惊奇的，这不禁让我想起来别人说的“苹果的保值性”，确实奢侈品就是应该保持高端，不论它到底有没有用值不值这个钱，不然接盘侠就太难找了。作为替代，也让我心痛的是，入手了一个ipadmini7

我靠，苹果全家桶，一下凑出了三个(三个国补用光光，全都给了苹果)。等等，先别急，我可不是胡乱选择的，首先当前最轻的且比较新的平板，也只有这个了，单凭这一点，我就已经没有选择了，至于galgame的方案，没错，我采用了大家乐道的串流方案。当然小还是有一定界限的，小到一定程度，不就变成手机了吗？就和手机一样，我之前也觉得“一直追求极致的小还是算了吧”，因为这样还不如直接用智能手表算了。或许用来区分只能手表、手机、平板，最为直观的应该是屏幕比例和握持手感了，手表方方正正(戴于手臂)、手机横窄竖宽(单手握持)、平板趋于电脑(双手支撑)，至于电脑必定是脱出的，即键鼠加持下的生产力了。现在的我玩过各种尺寸的手机，所以可以说，6.1寸的手机是我当前最喜欢的，至于更小的我以前玩的老手机其实就是了，太小的话，信息流容易缺少，体感并不是很好。扯远了，反正目前体验下来平板挺好的，或许最失败的地方就是这颗芯片了。
说到这个，我觉得当今手机的评测还是太失败了，芯片性能拍照啥的成为了主要项，我觉得这些东西还是放在芯片评测、相机评测上更好，因为手机的核心功能并不在这里啊！影像咱不懂就不讨论了，但可以拿芯片性能说说事，他们全拿起了各种3D高渲染游戏，说实话，这么小屏幕上我还要啥高画质…哦，难怪现在手机屏幕都变这么打了。说实话，电脑上玩高画质游戏比手机不知道舒服多少倍，我唯一会用手机玩的时候，无法两种情况，一是它没有PC的迫不得已，二是出差没法带上。但是只是从能玩的角度，好像是个现代的手机就能做到，比如我以前的用低端十几nm芯片的山寨机，都运行过原神和崩坏3，甚至还玩了很久，你就说够不够吧(能效比或许是芯片性能最有用的一点)。又扯远了，我觉得比起性能焦虑，很多实用的功能更需要考虑，比如系统自带地图软件。除了苹果和华为，我就没见过哪个手机做了自己的地图软件，虽说华果在国内用的好像是navinfo和高德地图的数据，但它们确实简洁实用啊。而且更重要的一点是，出了中国大陆，它们还能自适应切换并提供导航功能，这是绝对的加分项。当然频繁离开大陆也不太实际，当论地图这个功能，诚心而论，我觉得苹果的确实好

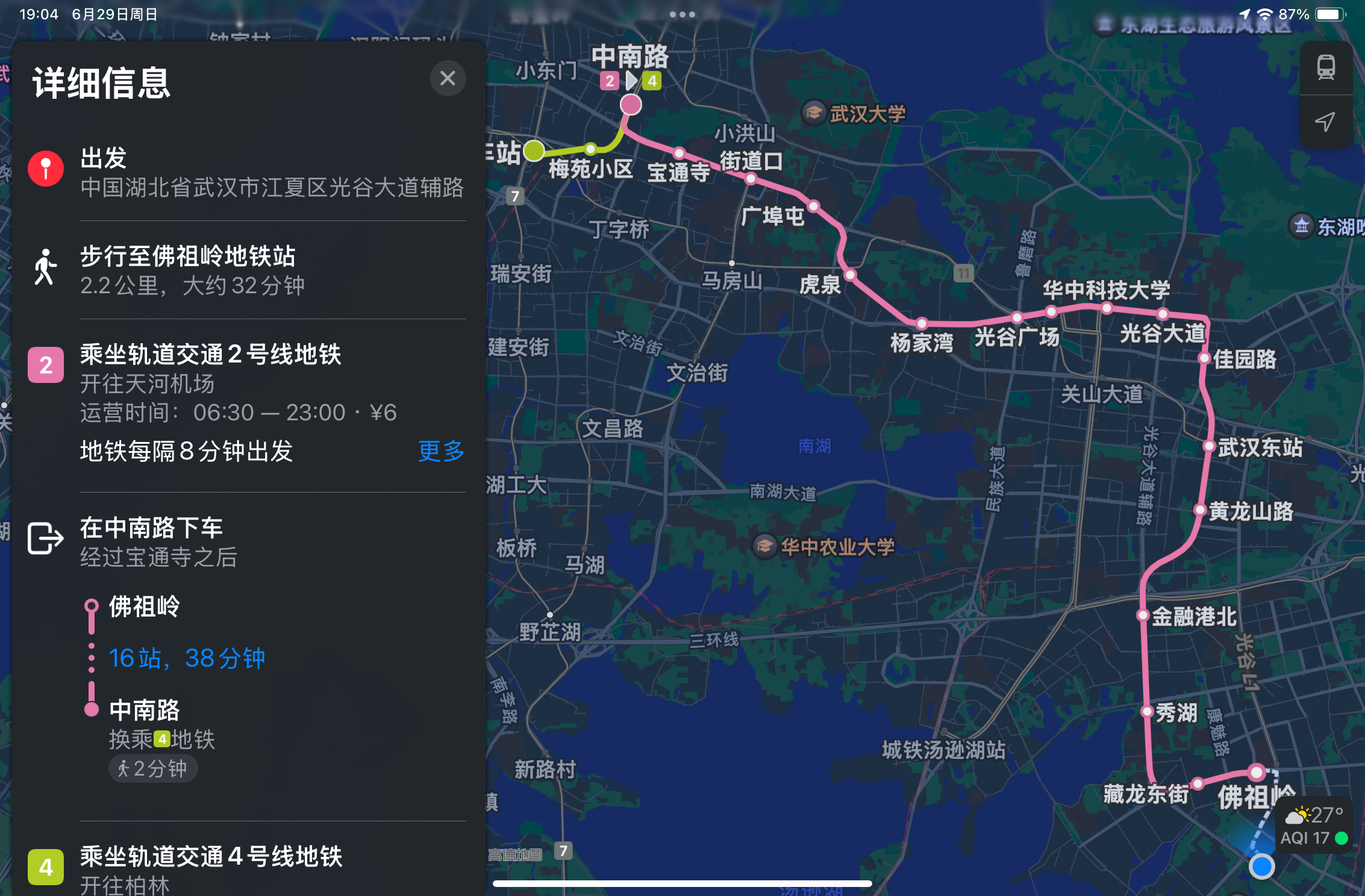
因为我比较喜欢用公共交通，上面一张图，就已经说明了我的偏好。当然iphone在实用性上难崩的一点就是，没有红外和nfc功能有点阉割，我说的阉割主要是指门禁之类的功能，因为Osaifu-keitai这玩意，只能说是日本的原因，为了这玩意搞个iphone，我觉得并不值得。大家所说的信号分为两种，定位和通信，对于前者必须最高的多频，单频GPS和双频GPS的差距还是挺大的，至于后者频段多一点自然好，但没必要硬闯，大多手机自带的漫游流量(华为天际通、小米全球上网等)足够应对短暂出国了，点名批评苹果！续航，这才是痛中之痛，其实我挺希望能多余的影像堆到电池上去，这样小屏也能多一些续航了，这时突然可以发现高制成的芯片有较好的能效比，对续航影响还是挺大的，一加13t是个不错的开拓者，但我觉得还不够。很多时候，报复性消费也只是为了填补童年缺失的遗憾罢了，真正到手以后，就会觉得也就那样。哎，只能说，找到一部合适自己的手机实在太难了，这不是自适应，而是在需要与舍弃之间被迫抉择之后的无奈。
最后再讲讲lean4吧，这东西确实越用越爽，在tactic模式下，有各种一键指令，其中simp(还有linarith、ring、tauto等等)如同易得版好用，其实啊，它可以让我们的思维变得更加严谨和细致，我印象最深的就是一个自然是的例子

1
2
3
4
5
6
7
8
9
10
11
12
theorem pow_two_le_fac (n : ℕ) : 2 ^ (n - 1) ≤ fac n := by
  rcases n with _ | n
  · simp [fac]
  induction' n with n ih
  · simp [fac]
  calc
    2 ^ (n + 1 + 1 - 1) = 2 ^ (n + 1 - 1 + 1) := by simp
    _ = 2 ^ (n + 1 - 1) * 2 := by apply pow_succ
    _ ≤ 2 ^ (n + 1 - 1) * (n + 2) := by simp
    _ ≤ fac (n + 1) * (n + 2) := by simp at ih;simpa
    _ = (n + 2) * fac (n + 1) := by simp [Nat.mul_comm]
    _ = fac (n + 1 + 1) := by simp [fac]

这是我自己写的一个证明，采用了更为直观的计算路径，但它最初的样子不是这样，当我们自然而然地使用数学归纳法时，会变成这样

1
2
3
4
5
theorem pow_two_le_fac (n : ℕ) : 2 ^ (n - 1) ≤ fac n := by
  induction' n with n ih
  · simp [fac]
  calc
    2 ^ (n + 1 - 1) = 2 ^ (n - 1 + 1) := by simp

结果你会发现，这么简单的一个式子，怎么都simp不过去，当时我也挺纳闷的，还打算一步步来得了，结果还是过不去，直到apply定理的时候发现

1
Nat.sub_add_cancel {n m : ℕ} (h : m ≤ n) : n - m + m = n

哭笑不得，自然数的减法还得考虑越界的问题，果然还是受了默认整数的诅咒呢！其实就使用体感而言，lean4中最困难的部分还是，集合论与类型论之间的跨越，虽然1 : ℕ的写法一出，很容易产生就是1 ∈ ℕ的错觉，但很快你就会发现后面的写法lean4不认，因为lean4认为ℕ是类型不是集合。当然如何直接把类型看成集合，好像已经可以做很多事情了，群环域什么的根本不再话下，但这种思维会让人在关键的时候捉襟见肘。一个简单的例子

设是元有限集，证明幂集在对称差集运算下构成域上的线性空间。

很显然，这并不能把集合类型化，幂集对称差集啥的类型论中并没有，当然类似替代是能做到的，比如把所谓的幂集看成一个二元值函数类型

1
2
3
4
5
6
7
variable {α : Type}
#check (α → Bool : Type)

#check (Fintype α → Bool : Type)

variable {β : Fintype α}
#check (β.card)

但是再去搞各种集合的运算就多少有些自讨苦吃了。看看mathlib库是怎么做的，对于子集搞了个子类型，但里面的carrier似乎宣告了集合论的难以离开，但是从下面性质来看的话

1
theorem mem_setOf {a : α} {p : α → Prop} : a ∈ { x | p x } ↔ p a

集合论只是用来宣告一种性质，当然对于更复杂地依赖集合运算的拓扑，它还是直接搞起了集合论。好吧，那么集合论和类型论到底如何切换呢？实际上集合的定义已经告诉了你

1
def Set (α : Type u) := α → Prop

“Prop=Sort 0”比“Type=Type 0”低一级，是能作为类型后缀的最低一级，这其实就是mem_setOf性质的来源，“α → Prop”则会升一级，因此无论如何都不会比Type低，从而可以作为一种类型，融入到各种依赖于类型定义的群、环、域之中。这样说还是太抽象了，就那我上面说的定理来说事吧。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
variable {α : Type} [DecidableEq α]

-- ℘是加法交换群
instance instVectors : AddCommMonoid (Set α) where
  zero := ∅
  add s t := s ∆ t
  zero_add s := bot_symmDiff s
  add_zero s := symmDiff_bot s
  add_comm s t := symmDiff_comm s t
  add_assoc s t r := symmDiff_assoc s t r
  nsmul := by
    letI : Zero (Set α) := ⟨∅⟩
    letI : Add (Set α) := ⟨(by intro s t;exact s ∆ t)⟩
    exact nsmulRec

-- ℘是F_2上的线性空间
instance instModule : Module (ZMod 2) (Set α) where
  smul n s := if n = 0 then 0 else s
  one_smul s := rfl
  mul_smul a b s := by
    show (if a * b = 0 then 0 else s) = (if a = 0 then 0 else (if b = 0 then 0 else s))
    by_cases h : a = 0
    repeat simp [h]
  smul_zero a := by
    show (if a = 0 then 0 else 0) = 0
    simp
  zero_smul s := rfl
  smul_add a s t := by
    show (if a = 0 then 0 else (s + t)) = (if a = 0 then 0 else s) + (if a = 0 then 0 else t)
    by_cases h : a = 0
    repeat simp [h]
  add_smul a b s := by
    show (if a + b = 0 then 0 else s) = (if a = 0 then 0 else s) + (if b = 0 then 0 else s)
    fin_cases a
    repeat simp
    fin_cases b
    · simp
    simp;symm
    calc
      s + s = s ∆ s := rfl
      _ = 0 := symmDiff_self s
      _ = if (1 : ZMod 2) + 1 = 0 then 0 else s := by
        have : (1 : ZMod 2) + 1 = 0 := by
          group
          rfl
        simp [this]

过程挺普通的，唯一值得注意的是集合和幂集的实例没有出现，按照常规思路，我们可能会这样给出定理

1
2
3
4
5
6
7
variable {α : Type} [DecidableEq α] (Ω : Finset α)

def ℘ : Finset (Finset α) := Ω.powerset
def n : ℕ := Ω.card

instance instVectors : AddCommMonoid ℘ := sorry
instance instModule : Module (ZMod 2) ℘ := sorry

然后你就会发现连给出定理都做不到，如果单纯从定义角度来看，原因很简单，因为℘不是类型，但如果从集合就是类型的角度来看，瞬间就奇怪了起来。或许看一些更加实际的东西会更有效一点，我们知道1 ∈ ℕ是不合法的，但如果非要有效起来，可以像下面这么搞

1
2
variable (s : Set ℕ)
#check (1 ∈ s)

明白了吧！所谓的类型实际是主观概念，一个简单的例子集合，我们可以认为它的元素有整数、小数和超越数三种，也可以认为它只有一种实数

1
2
#check ({0, 1, 2} : Set ℕ)
#check ({0, 3.1, 2} : Set ℕ)

上面一句是合法的，下面一句并不合法。好！回到我们的例子，由于我们现在的集合是一种抽象集，其元素没有什么具体的类型，因此我们使用通用类型(α : Type)和集合代表(Ω : Finset α)或许是一种方法，但我们实际可以更灵活一点，我们直接将Ω中的所有元素视为一种类型，因为这里的整数n其实没啥作用，甚至n元有限集也没啥用，可以直接扩展为所有集合，这样的话类型(Set α)相当于Ω的所有子集，也就是所谓的幂集，它的实例就是幂集的元素，这样解释的话，证明有没有合理很多？
好啦，好啦，就这样解散吧！