渲染这东西，学得真的简直不要太无聊，重复的东西学一遍，再仿写一遍代码，最后呢？还是得用别人封装好的东西来应用于实际的开发，我一直很疑惑，渲染这玩意除了硬件上升一个层数，算法真的有优化的余地吗？当然我认为的实际的情况是，如今的渲染已经基本满足需求了，不过事实如何，那就不得而知了。

非欧几何

今天想讨论的主题是非欧几何的渲染问题，注意我们不会提及光照相关的东西，因为笔者都还在学习呢！而我们现在的目标是弄清非欧几何是什么？泛泛地来讲，不是欧式几何的都是非欧几何。稍微学过几何的人会认为，依欧几里得第五公理的不同，而产生的双曲几何(又称罗巴切夫基几何)，球面几何(狭义黎曼几何)，称为非欧几何。其实都不能算错，关键在于怎么看待它，我们需要提两个要点，首先单纯从公理的角度，欧几里得的五条公理并不完备，大多证明依旧依赖直观，而完备的公理体系应该是希尔伯特在几何基础里所给的五组公理。其次，黎曼几何是微分几何里十分重要的部分，不单只是球面或者椭圆上的几何。相信许多了解非欧几何的人，都喜欢在球面或伪球面上进行思考。确实如此，这也是如今对非欧几何的一个统一看法，那为什么常被讨论的非欧几何只有两种呢？符合直觉的一个很重要的点就是性质不随位置改变，比如三角形不论放在哪里内角和都是固定的，170、180、又或者190之类的。注意我们只在2维的平面上，所以考虑模型的时候则是3维空间中的曲面，要求各点性质不变其实很复杂，关键在于什么样的性质，比如Gauss-Bonnet公式表明了角度和与测地曲率和高斯曲率的关系，由于我们通常将曲面上测地线选取为直线，所以内角和实际只要求高斯曲率为定值。在通常认知下，区分非欧几何的平行公理，实际也与角度相关，所以我们一般认知的非欧几何就正好对应高斯曲率为正定值和负定值的情况，而高斯曲率为零就要注意了，不单只有平面，还包括柱面锥面等可展曲面，依据是否有脐点还有进一步的区分，就不讲了。数学很神奇，也很复杂，你只要考虑十分理想的情况就行了，常高斯曲率我们就分三种情况，平面、球面和伪球面。对于一些拥有奇特性质的几何可以放在高维欧式空间来理解这一事实，其实是有数学定理支持的，Whitney浸入定理和Whitney嵌入定理，通俗来讲就是，能计量的几何(局部欧式化的流形)可以对应到更高维欧式空间的图形上。比如，二维的罗氏几何可以对应到三维欧式空间的伪球面(也称双曲面，本质是高斯曲率为负常数的旋转面)上的几何。说了这么多，总结就两句话，非欧几何十分多样不只两种，一般的非欧几何都可以在更高维的欧式空间中表现出来。

两个项目实例

在Github上，我随手搜了一下NonEuclidean，然后挑选了比较有代表的两个来讲讲吧，当然项目太老，OpenGL版本太低，我的电脑运行不了，只能看他们的演示和源码了，项目1和项目2。

项目1

直接给结论，这大概和非欧几何没有关系。这个项目的关键部分是下面这个Portal类，

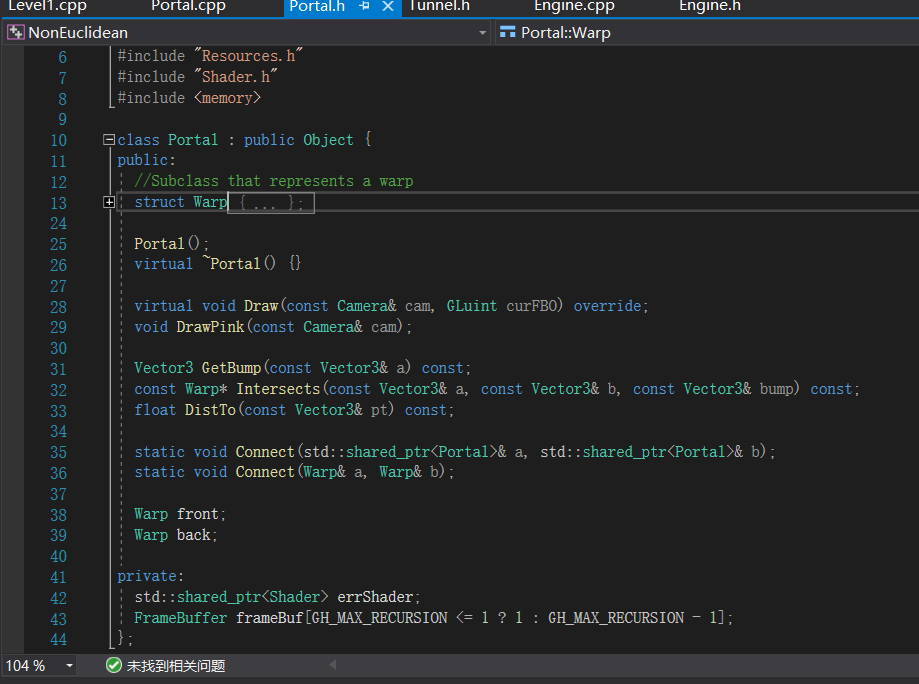
我们来详细讲讲它到底能做些什么，它是Object类的子类，Object是所有渲染对象的父类，提供了它们所需的共有属性，如位置、旋转和缩放，包括绘制，而Portal则拥有着独特的绘制函数，也因此使它成为了整个项目的核心。这里稍微提一下，这个项目的渲染循环，

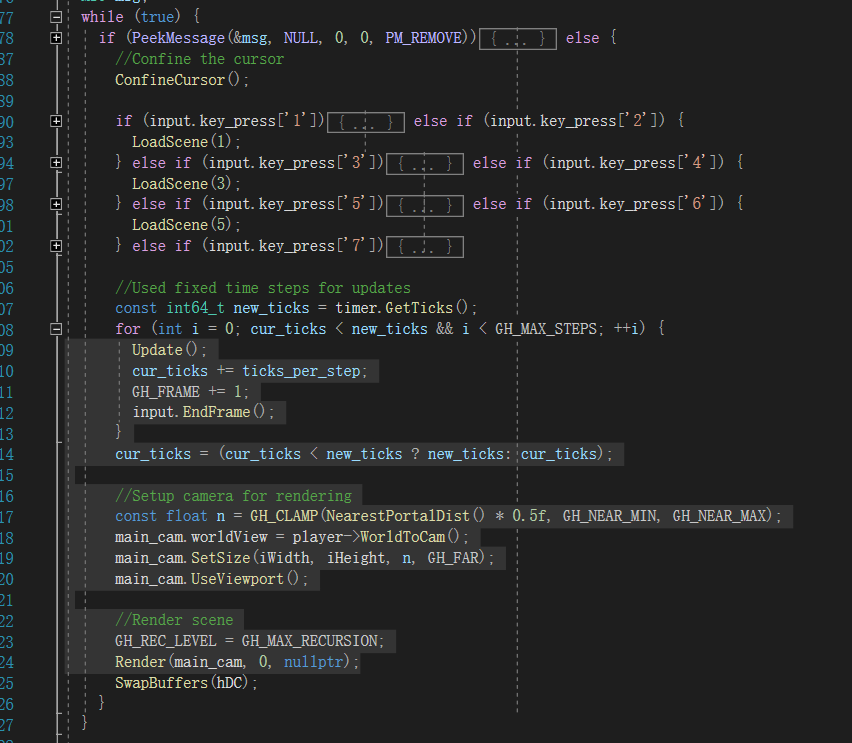
我们可以看到关键在于两个函数Update和Render，前者将当前的参数计算好，后者将实际画面绘制到屏幕上。从下面的Render代码，

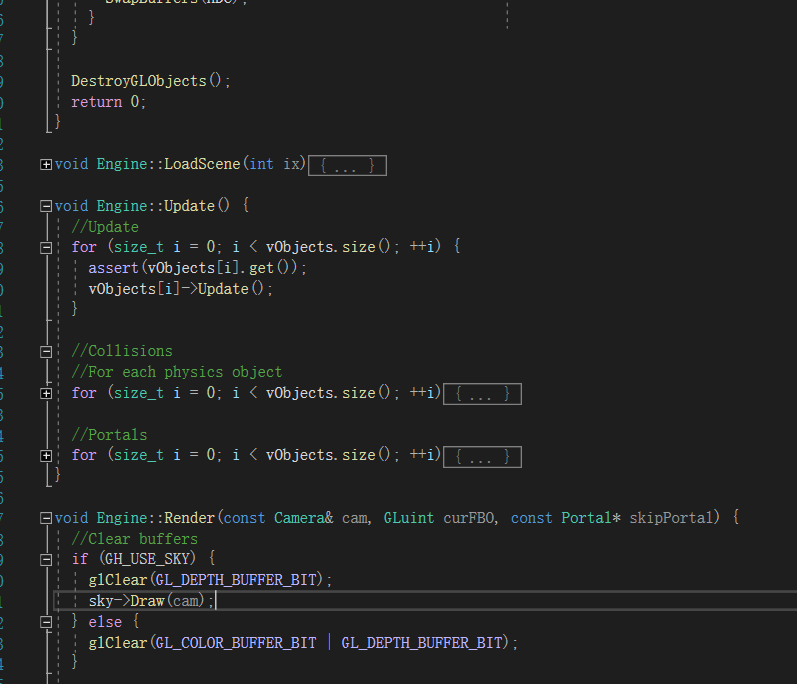
我们可以知道，它完成了两件事碰撞处理和Portal相关处理，对于前者主要是下面这个情形，

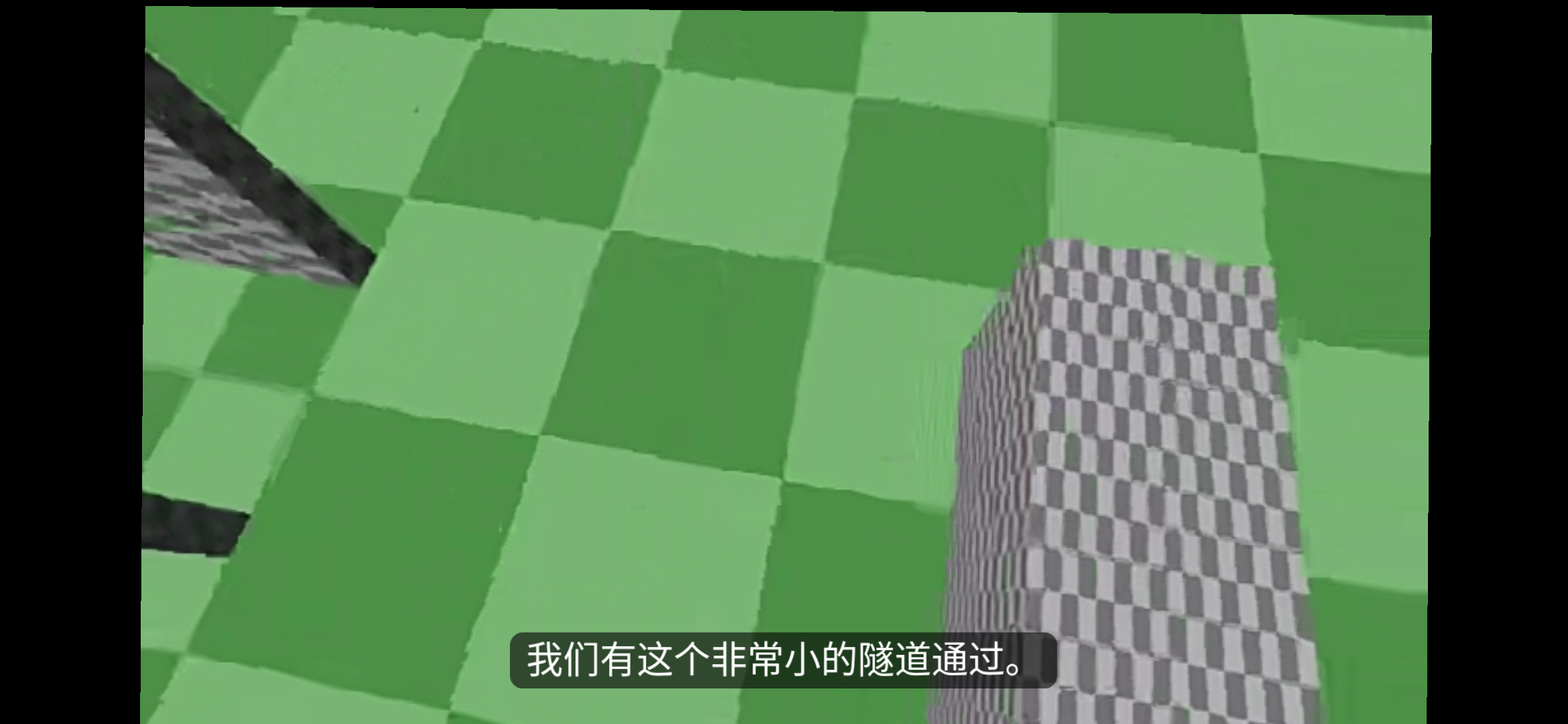
即玩家体积过大，进不了小洞口，而Portal的处理则与Portal的功能相关。所谓Portal实际上是一个传送门，而这个传送门可以看到对面的景象，我们拿第一个例子来说明，演示如下

代码如下

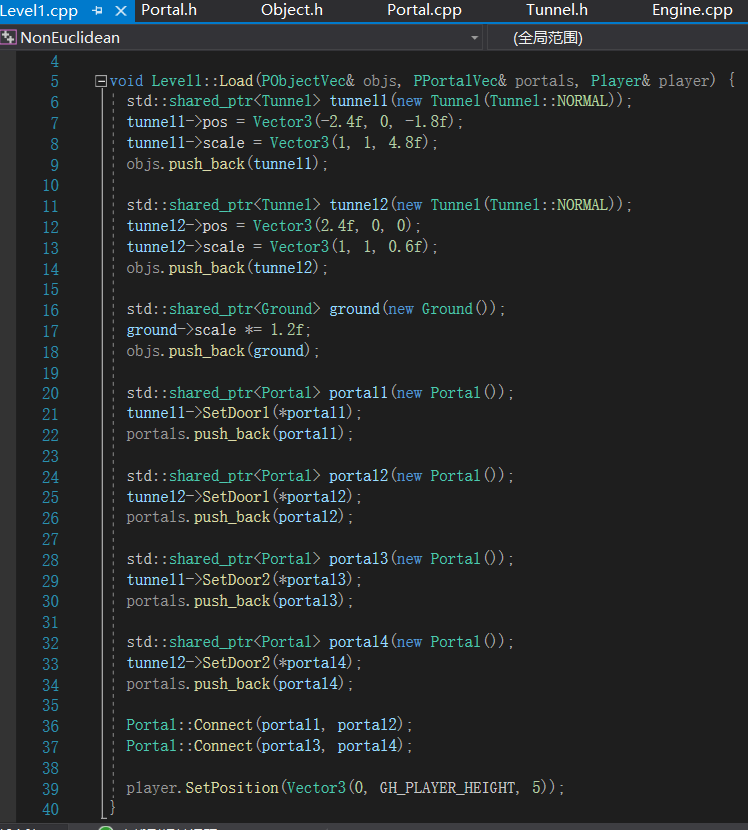
我们可以看到，它安排了两个Tunnel(隧道)和四个Portal。隧道可以设置两个Portal，两个Portal之间可以Connect，仔细看代码，我们可以发现隧道的两个Portal并没有连接，而是与另一个隧道的Portal连接。什么是连接(Connect)，Portal又是什么，我们还是得看它的源码。Portal有两个面front和back，使用Warp进行封装，而Warp保存这个面的所指向的两个Portal，表示从哪里来又到哪里去。总的来说一个Portal可以连接两个Portal，分别放在两个面上，至于它对应的模型“double_quad.obj”，在blender里打开可以得到，

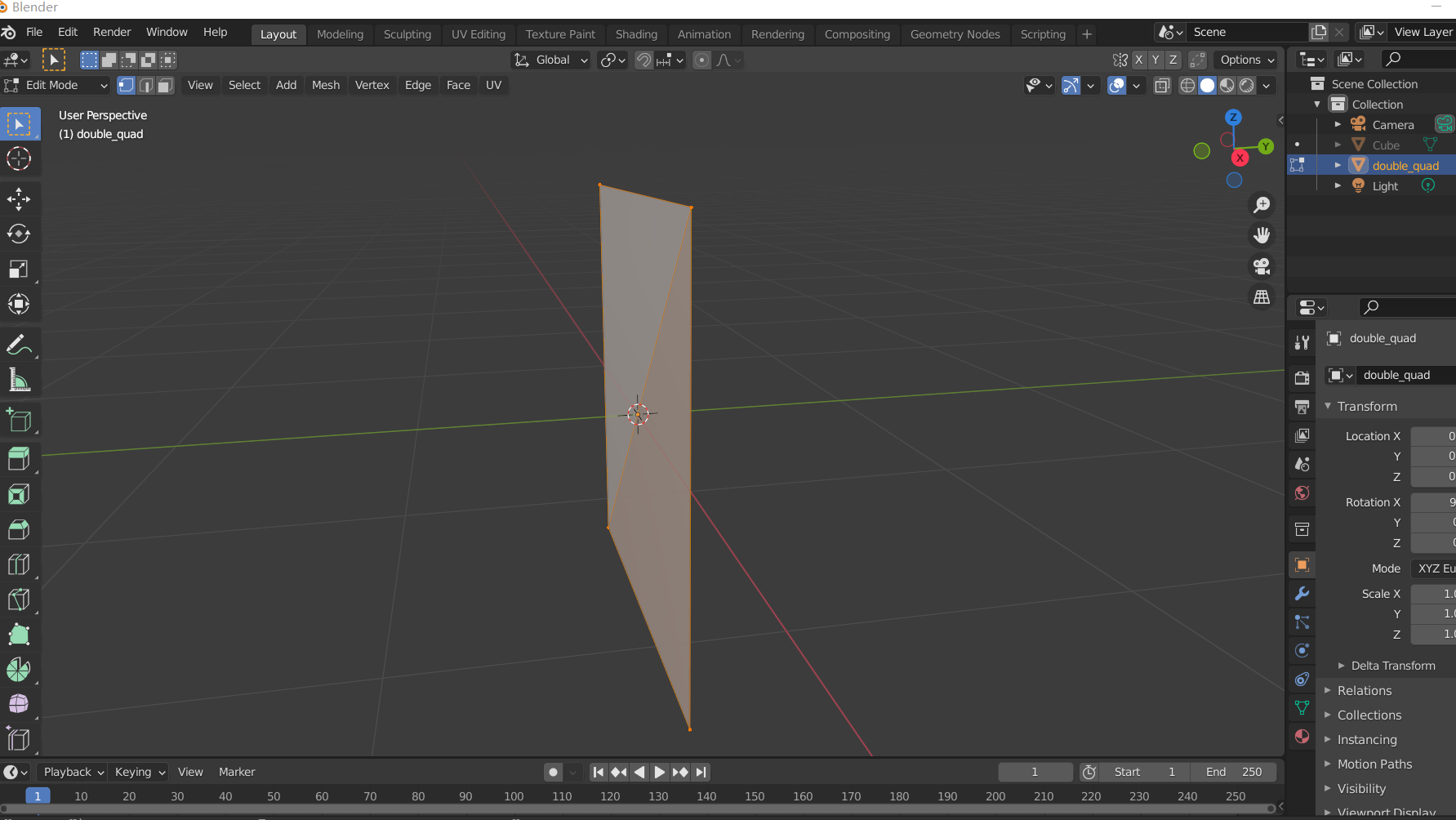
其实就是一个矩形，没有厚度，有两个面，符合类的需求。我们稍微看一下Draw的代码，

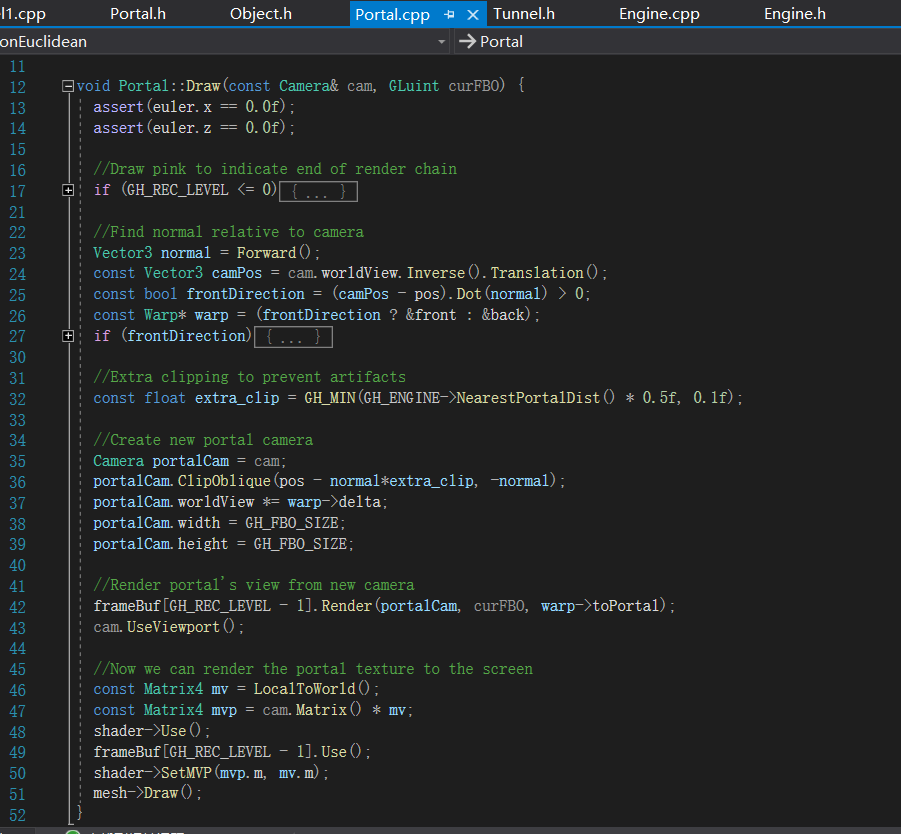
在42行，我们可以看到一个关键的技术——帧缓存，这个功能很好理解，可以把它理解成一个可以放在任何位置的实时照片，代码层面就是渲染某个场景后将它保存为贴图，放到另一个渲染场景中去，这也是实现Portal的关键。首先是测量我们处于Portal的前面还是后面，接着到相应的目标地来建立相机，然后渲染场景保存到帧缓存中，最后完成当前Portal的渲染。所以，我们在front面可以看到toPortal所在位置的画面，在back面可以看到fromPortal所在位置的画面。其实进入Portal的时候，也是会实现传送功能的，就是改一下Player的位置就行了，而检测发生在我们之前提到的Update里面，

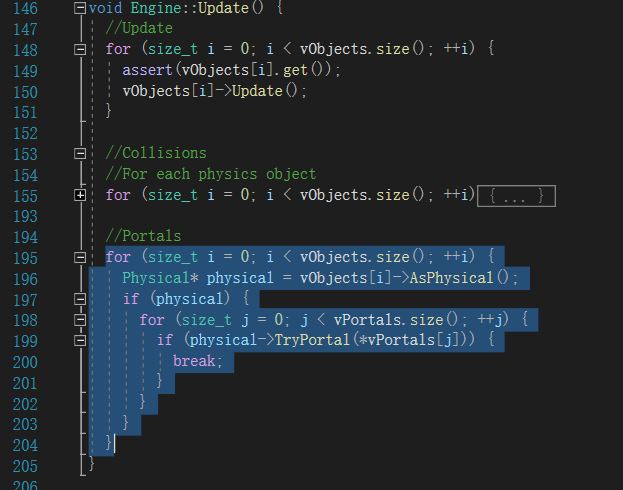
方法是比较常规的遍历，首先遍历所有的Object，前提它是Physical，目前只有玩家具有物理性，然后对每个Portal进行碰撞检测，不算优秀但也不差。到现在，我们也可以还原第一个场景到底做了些什么了，如下图

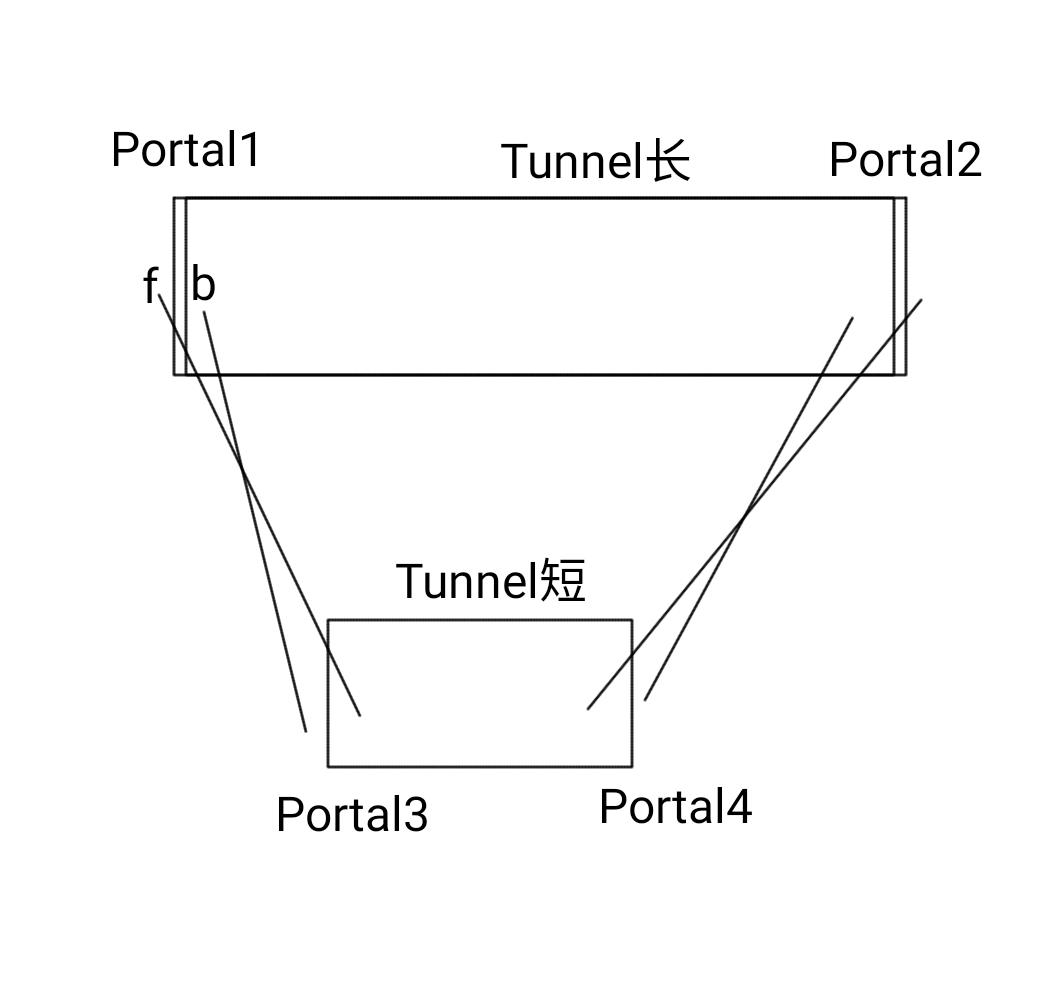
也就是空间本质上没有增减，只是内部空间从视觉上换位了，至于后面的几个场景本质都一样，只不过有时它会将多余的空间放到较远的地方，比如第二个Level2——将6个房间藏于4个房间内。其实Portal的原理在××门之类的mod里就有，也不是什么新奇的东西，只是帧缓存的一个用法，其实在演示的最后，

作者也提了一下Portal的原理，但讲得不是很深就是了。至此项目分析的差不多了，从纯数学的角度，它不是非欧几何，因为物质影响空间的性质并不合理，而应当是更纯粹的几何才对，当然你要和我说广义相对论的话，我只能说我了解的不够深入。

项目2

接下来的这个项目就的确有非欧几何的样子了，我们来详细地研读一番吧。因为涉及很多定量的东西，我们稍微回顾一下OpenGL的渲染流程和思想，然后再谈如何进行非欧的改造。

OpenGL渲染流程

现代的OpenGL渲染管线如下图

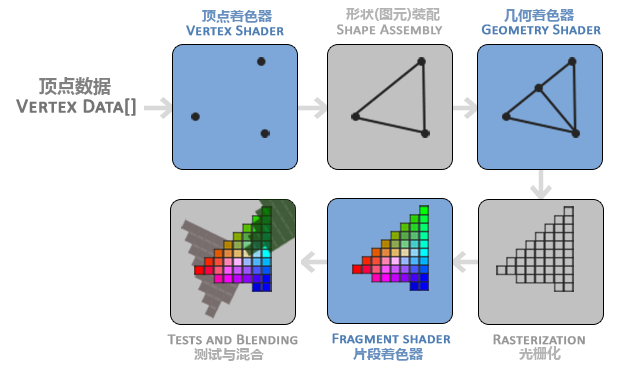
当然它并没有说清，如何渲染，又如何与代码产生联系的，只是单纯说明了渲染在GPU内的流程，其中蓝色表示可以控制的部分。拿出我之前在渲染游记中提到的例子，GPU渲染包含两部分代码，一是在CPU上的我们所运行的可以可以与GPU交互的程序，另一个是运行在GPU上的有输入和输出的程序，即着色器。OpenGL渲染就两步，设置状态参数和执行渲染命令，设置步骤拥有着最多部分的代码，如设置渲染的顶点数据VertexBuffer，设置渲染的Shader，由CPU向GPU传递Uniform等。
有关渲染我们需要注意几点，点的数据只使用规范化坐标，限制在正负一内；基本图只有点和线，并没有如圆一样的曲线；点或点组或片段是并行处理的，相互之间不太容易交流。在OpenGL由CPU传入的一个点可以存储不止3个数据，最大值由显卡决定，而最后确定顶点位置的实际是顶点着色器的输出，是一个4维向量，也就是说传入顶点的实际作用是确定有几个点，执行了当前顶点着色器多少次，而传入的顶点用于区分是哪一次。为了说明这件事，我来举个简单的例子，如下，

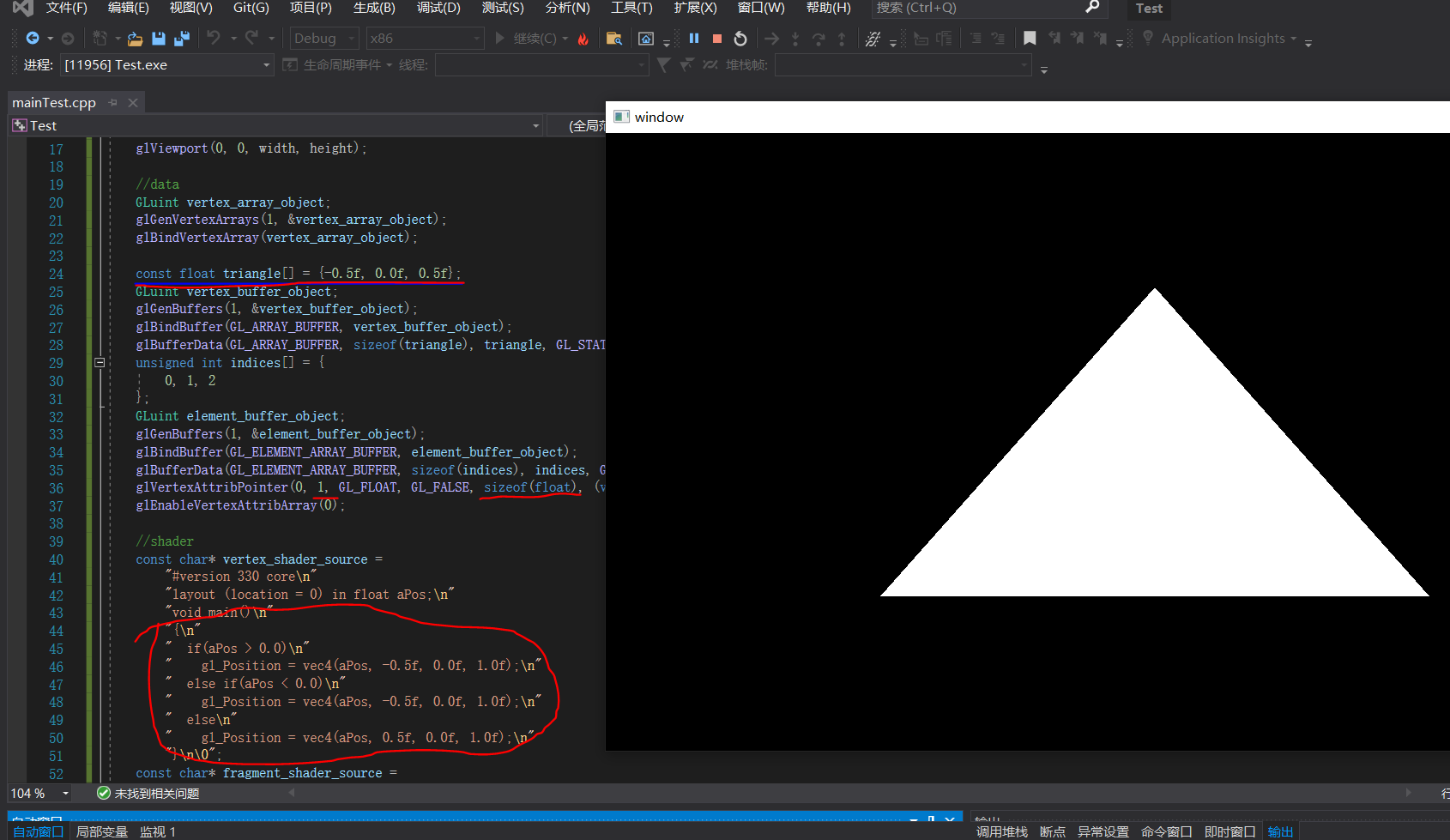
红色是原来例子的修改部分，可以看到VertexBuffer并没有提供完整的数据，而是顶点着色器中进行补全的，当然我们不推荐这样的做法，主要因为通常情况下，从模型中读取的顶点数据是在CPU中，不能直接传到GPU里去，而且在GPU中进行逻辑运算不是明智之举，这个实例主要用于说明顶点最终在顶点着色器中以四维向量确定。
gl_Position的寿命应该维持到了光栅化阶段，当然这是猜的，因为在几何着色器我们任可以操作gl_Position完成图元的绘制，不过依旧限制在正负一内就是了，而到片段着色器的时候只能使用gl_FragCoord变量确定位置，并且只有2个分量x和y，坐标是窗口坐标。实际上gl_FragCoord有个z分量，但主要用于深度测试，表示将什么绘制在前面。gl_Position到gl_FragCoord到底发生了什么呢？首先是，前三个分量分别除以第四个分量，z作为深度，而规范化的x和y则对应到屏幕上去，对应代码中的glViewport的区域。这里其实有说明了一个事实，OpenGL并没有3维识别的能力，而是将z作为谁在前面的指标，当然也可以对深度测试进行调参，这对以后透视视图的理解有一定帮助。至于为什么使用四维向量来表示位置，实际主要是便于运算，我们接下来会讲。

坐标系统

如果直接使用OpenGL的坐标系统是十分不方便的，比如坐标限制在正负一，随不同的屏幕会得到不同的效果，而且原生的绘制流程是平行投影，不能达到符合现实的效果。我们也很容易发现，单纯绘制二维图形流程也太复杂了，实际上这样的流程本来就是为3维图形服务的，而现在你拥有了修改源代码的权利罢了。而我接下来说的这套坐标系统，其实可能就是OpenGL1.x版本的源码，不过确定就是了，但这流程在哪里基本都是不变的。
我们知道顶点最终是在顶点着色器中确定的，所以我们最终的目的就是将我们的坐标系统变换到gl_Position所需要的规范化坐标去，输出结果是一个点，一个四维向量，输入存储在VertexBuffer里是一个不定维的向量，一般情况下我们只取前三位，其它部分用于保存如纹理坐标，法向量之类的数据，当前用不到就不管了，输入坐标我们经常会这么写vec4(aPos, 1.0)，aPos输入的坐标数据，这其实是渲染中的习惯，以第四个分量为1表示点，以第四个分量为0表示向量。相信搞过游戏开发的都知道对于一个实体，都有一个叫锚点(anchor)的东西，也称局部坐标，而我们传入的点集所处的坐标系正是这个局部坐标，这样对于绘制有许多便利之处。学过线性代数的同学应该知道，我们要将这个初始的四维向量变化到目标的四维向量是，如果要充分利用GPU的计算力，使用4*4矩阵进行乘法是比较便利的。大量的实践表明，使用下面的变化式是较为合适的

其中V表示向量，M表示矩阵。至于矩阵如何完成点的平移、旋转、缩放和坐标系变化，就真的没讲的必要了。矩阵从左到右我们依次称为投影矩阵、视图矩阵和模型矩阵，而这些矩阵通过Uniform由CPU传入GPU，首先，我们假想一个世界坐标，它单单只是数据，并不存在于OpenGL中，模型矩阵就是用于确定数据点集在这个世界坐标中的位置旋转和缩放的，也就是通过模型矩阵运算后，这个模型才真正确定，这样有一个明显的好处，如果绘制相同模型的图形时，我们只要一套点集数据，通过变化模型矩阵即可，这样可以极大的节约数据所占用的内存。视图矩阵则将世界坐标变化到视图所在的坐标(俗称相机)，通过对这个矩阵的调整，我们可以模拟在这个看似3维却不是3维的空间中自由移动。最后一个矩阵主要用于在这个视图坐标中圈一块空间，并映射到规范化坐标中去，平行投影与透视投影也是在这里实现的，也包括长宽比的确定，透视实现的方式并不难，只要将视线上的点的x和y坐标变化到相同即可，实际操作中用到了第四个分量，这样便于将视线上的点平分到正负一内用于深度测试，不过通常只用了正数部分，这样也符合常识。值得一提的是，裁剪其实是在几何着色器之后执行的，方法也很简单判断坐标是否在正负一内即可。

项目浅析

终于回到了这个项目，我要提前说一点，我对这个项目的光相关内容存在质疑，所以我们不考虑这部分，至于原因，先看看我对几何部分的说明。几何部分内容主要集中在顶点着色器上，我们来稍微看一眼，

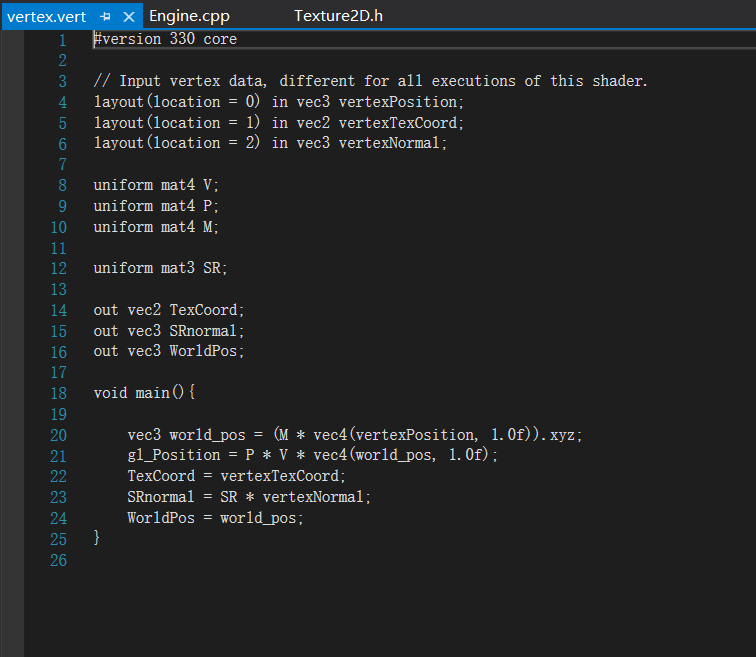
与传统算法相同，使用了3个矩阵来实现变化，也就是说这个项目主要是使用的矩阵与传统不同，来实现与传统不同的效果，我们可以在项目找到作者对此的解释

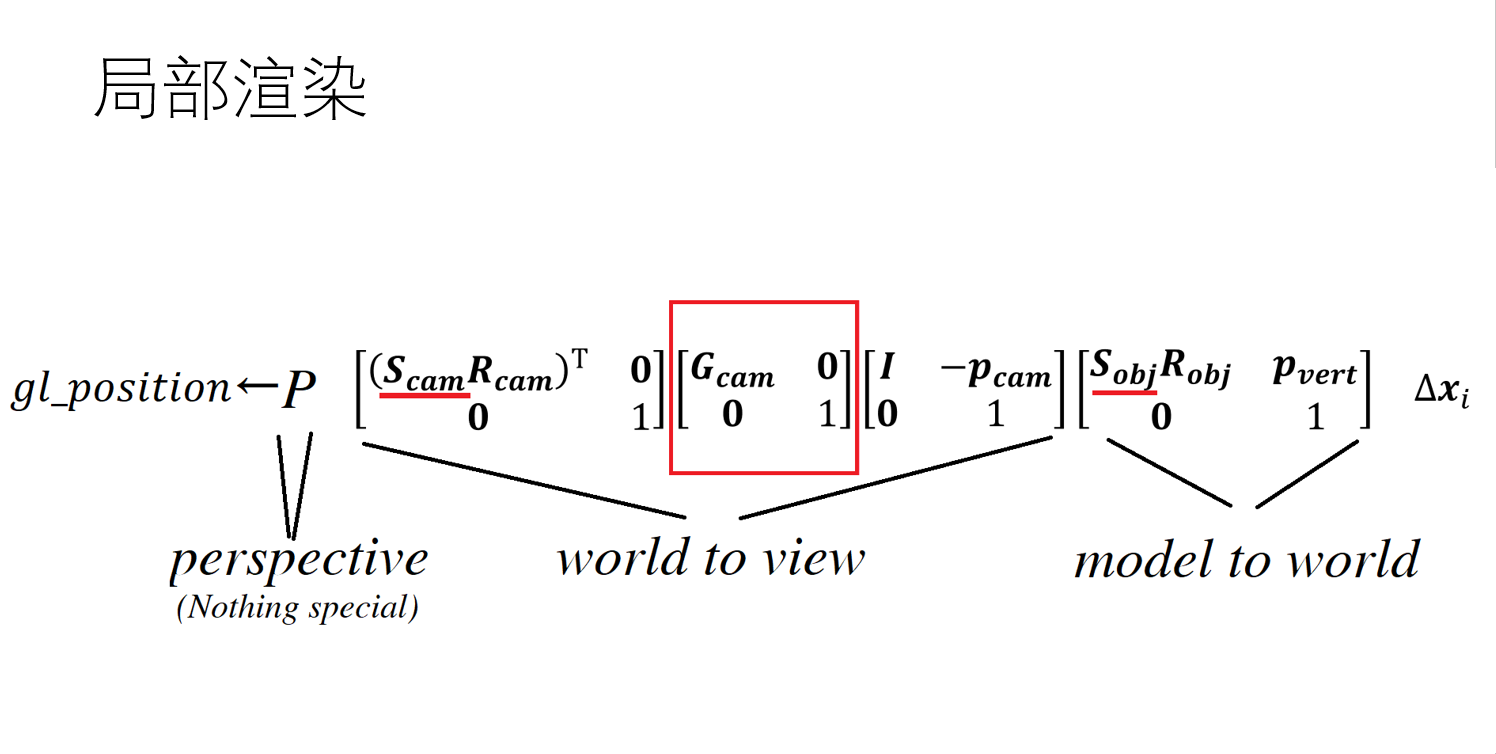
从中我们可以知道，作者只改变了视图矩阵和模型矩阵，这点也可以从代码中得到证实

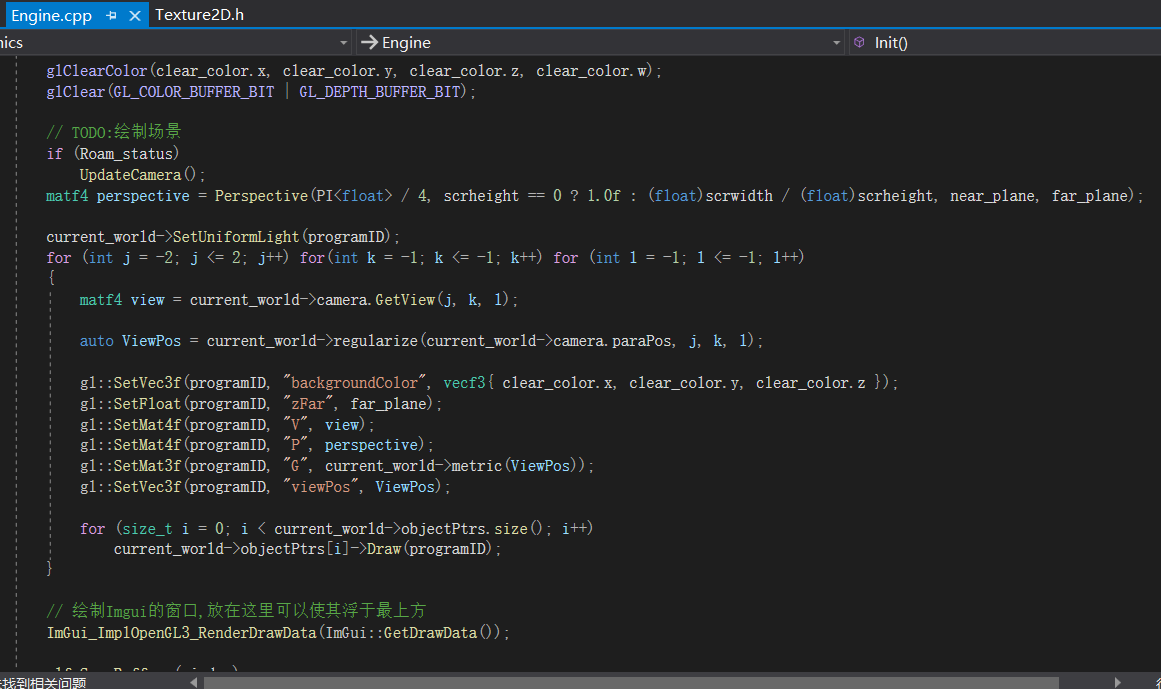
我们没有看到模型矩阵的传入，它实际是在Object的绘制中确定，Mesh的绘制中传入GPU的

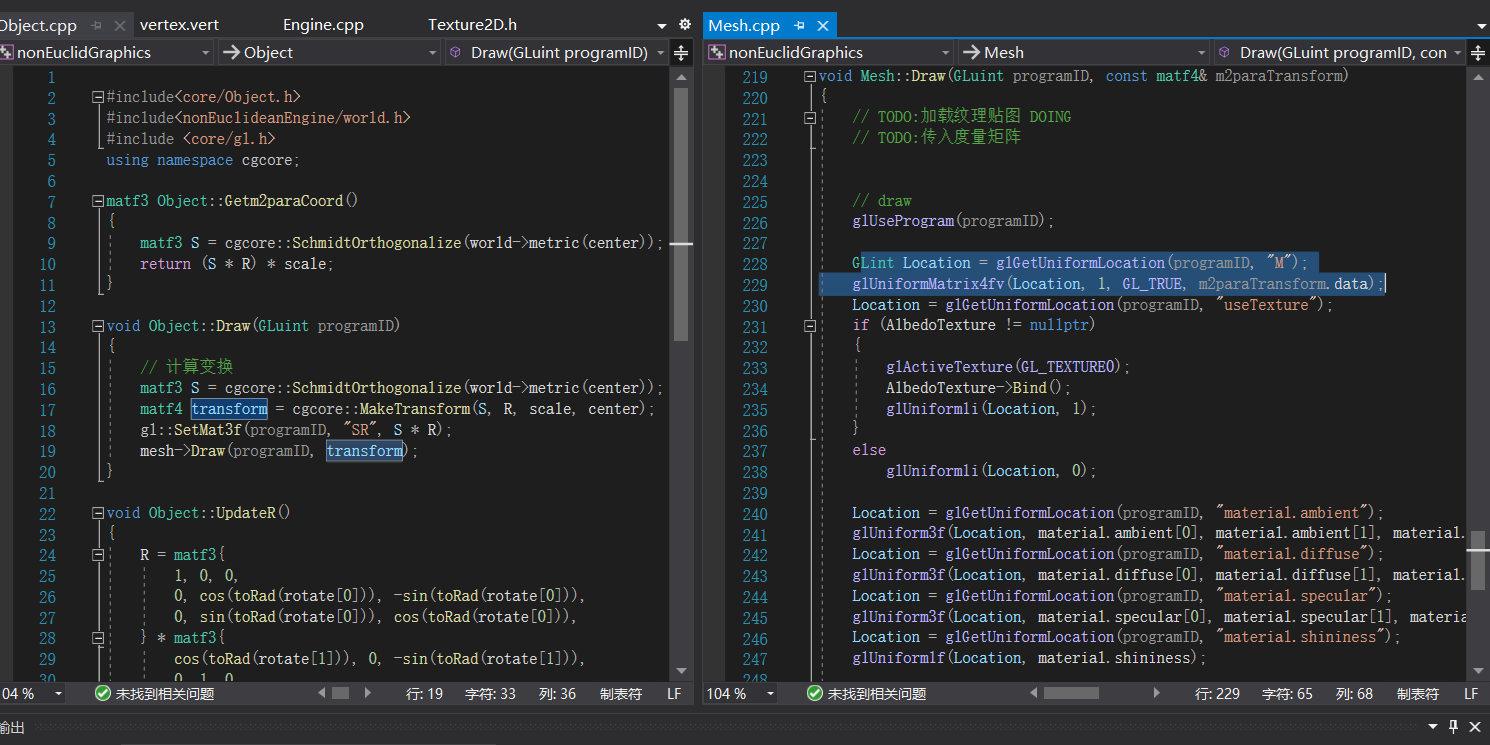
实际上，Object包含的是点集，表示一个模型，Mesh才是实际完成每个点绘制的，其实在这里就已经发现了一个项目问题，我们先推后一下，回到怎么确定矩阵的问题上来。
传统的模型矩阵主要包含位置(平移)、旋转和缩放的信息，并且在矩阵上也有一定的规律，平移信息位于矩阵右上3×1里面，如上图的p(vert)，旋转和缩放位于左上3×3里面，如上图的R(obj)，从如下代码

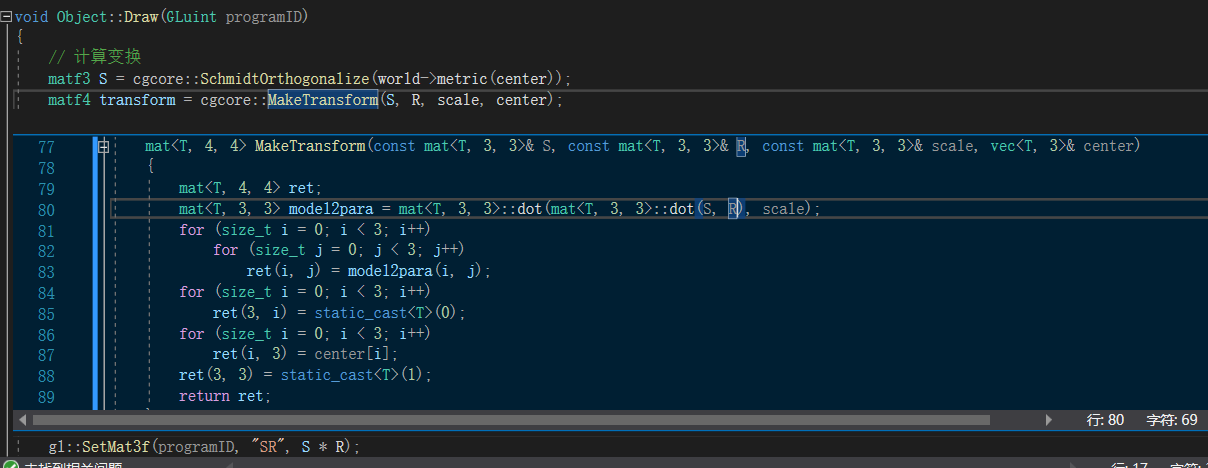
我们可以知道，这个项目其实就是让R多乘了一个3×3的矩阵S，而这个S被作者称为度规，对每点通过不同世界的metric来得到，值得注意作者的这个项目有好几个不同的世界。理论上来说，每点的S矩阵应该是不同的，但作者让每个Object的所有点都使用center点所对应的S，这就是我之前所说的可能问题。
对于视图矩阵，一般只有平移和旋转，分别表示相机的位置和朝向，由于朝向产生的方式有几种，所以一般分开进行相乘，下面是欧式空间下的生成方法

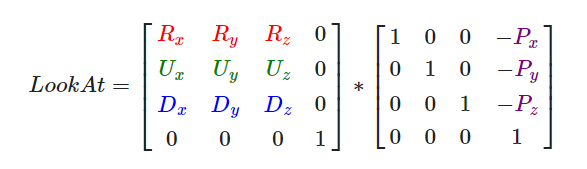
其中P是相机的位置，R、U、D分别表示右向量、上向量和朝向向量，它们可以组成一个正交标架，即坐标系，由线性代数的知识可以知道，只要像上面一样一排列，就可以实现世界坐标向相机坐标的转化了，而平常对相机的移动，可以通过位置向量加上相应的向量来实现，十分方便，如果要实现旋转的话，先看看这个项目

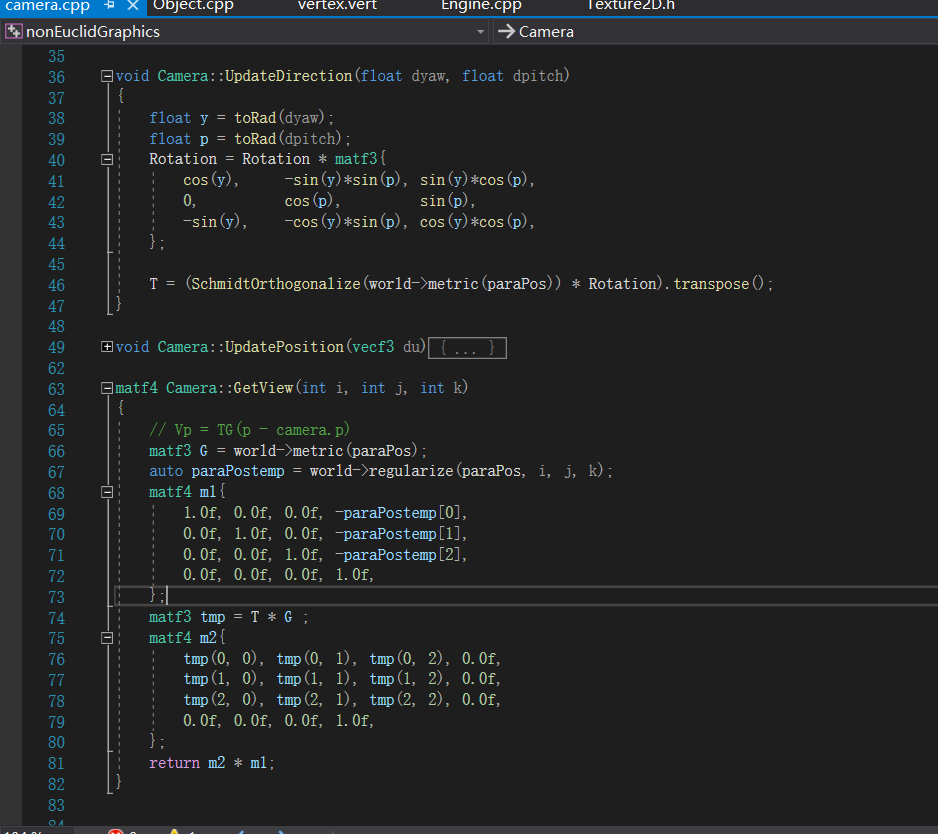
在UpdateDirection里面，我们看到一个矩阵Rotation，直接拿出来就可以实现我们平常的旋转了。而在这个项目了，我们发现，与Object类似，相机也同样是在旋转部分乘上这点的S矩阵。而在这个项目中，视图矩阵并不是作者所展示的那样有三个部分，在上面的getView可以看到，最右边矩阵m1是相机位置，不过多进行了一个叫regulariaze的不明操作，这个等下讲，而m2显然不是作者图给出的那样，在getView中可以看到结果是T*G在3×3部分的转置，在UpdateDirection可以看到T是S矩阵与旋转矩阵R乘积后的转置，而S与G的差别只是是否进行了施密特正交化，化简后是G的转置乘R乘T，所以此项目视图矩阵的差别就是旋转矩阵进行了一次相和变换，而且两个矩阵还差了个正交化，下面是作者在另一篇文章中的设想

这倒是符合代码中所写的那样，当然乱七八糟的，我看不懂，大致是前半将如何实现lookat，后部分说明为啥需要S和G，总之不明前后关系和内容。要不我们先来看看这个相机的移动吧，这是代码

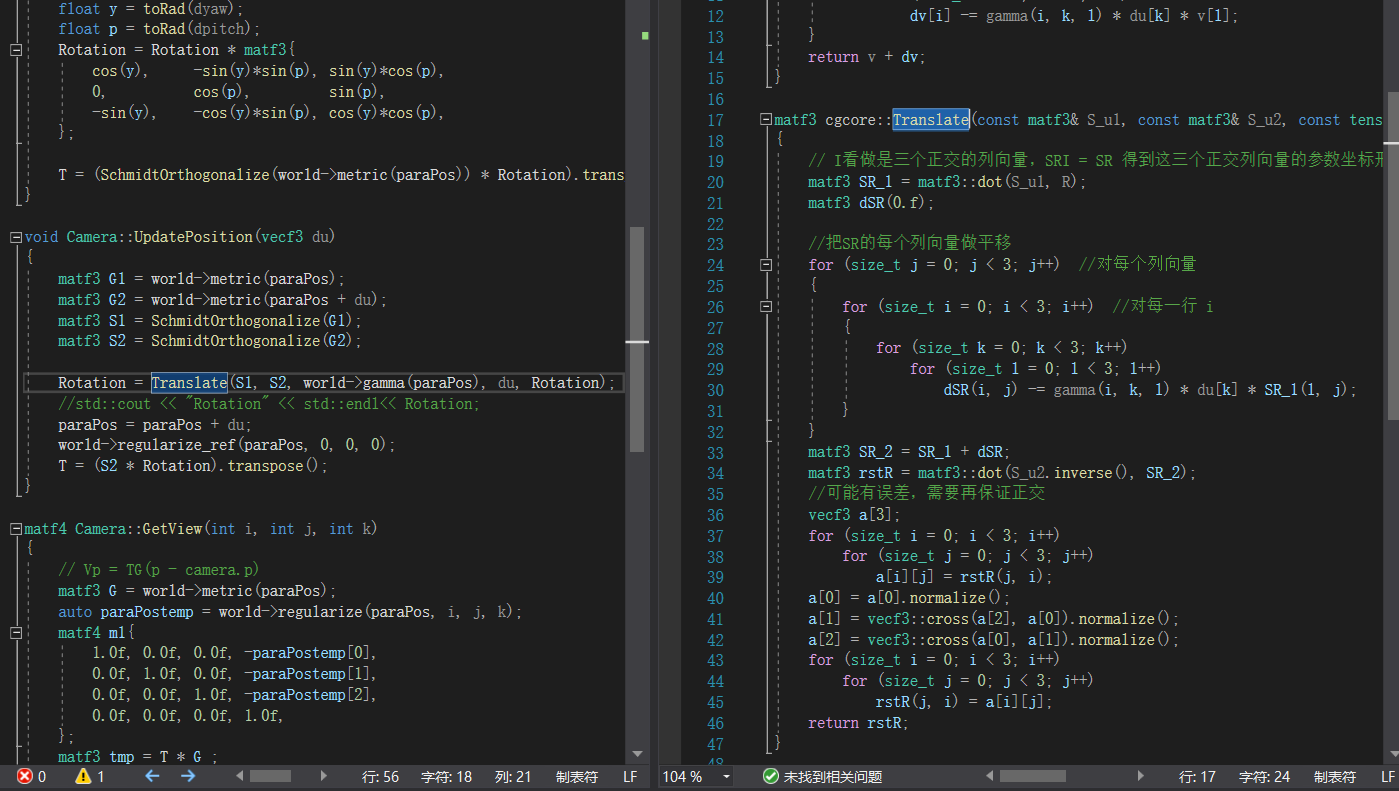
首先它取出前后两个不同位置的矩阵S1和S2，一系列复杂操作得到Rotation，更新paraPos和T，但是这都不重要，虽然在Engine里先更新方向在更新位置，但是对于位置长期传入的是零，移动后占主导的仍然是方向更新，所以这里面真正起作用的就paraPos的更新，移动du然后regularize一次。

项目总结

至此我们将整个项目的结构看完了，有几个疑点，首先最开始的物品坐标指的是什么，是曲纹坐标，还是参数坐标，还是欧式坐标。我们稍微解释这三个坐标的区别，4维空间中的3维流形，有可以由三个参数确定，无任何限制时，这三个参数就是所决定点的参数坐标，而参数如果正好是测地线的弧长参数，就称为曲纹坐标，而在4维空间中的坐标就称为欧式坐标。显然坐标只有三个参数，不可能是最后一种，从WorldExample里计算度规(我喜欢叫做度量张量)的方法可以看到，并没有选择弧长参数，只是直接拿常见的一般方程来进行计算，其实这样选择的坐标是不符合要求的。而regularize只是单纯执行取余，比如在球面上绕一圈回到原点，在视频演示里也说了一种所谓的循环空间，就是这么来的。回到渲染流程上来，让模型矩阵莫名地乘以一个度量，实在不知道有什么用处，度量张量的核心作用是确定微分长度的，要乘也是要乘以位置的变化，这么说起来，它给的错误局部渲染图确实是这么写的，但代码里却又和这没什么关系，相机部分也懒得继续说了。总得来讲，我认为它只是玩了一些数字魔法，随便乱乘得出了一些奇妙的效果，再配上非欧几何之类的公式计算，使它看起来是如此的合理。

非欧几何渲染

从我的角度来看，非欧几何渲染是否可能取决你到底怎么看待它。如果只是要反直觉的话，前面两个项目其实都是可以的，而且后面一个项目还会更加的真实一些。渲染的核心几何元素是点和线，几何的核心元素也是点和线，如果单纯看着我们的屏幕，把很直的线当直线，我们永远只能看到欧式几何，如果你愿意把曲线当直线，当然就可以看到符合非欧几何的现象了，但是从OpenGL的渲染流程来看，直线变曲线并非可能的事，除非每条直线你都愿意给足够多的点，这主要是针对一些不太均匀的空间，每点有着不同的度量张量。要知道我们只能看到欧式空间，除非高一些维度做投影，这里我要提一下Whitney浸入定理，它其实是有定量关系的2维流形可以浸入3维欧式空间，而3维流形则最少要浸入5维欧式空间，对于只使用4个分量的OpenGL其实是不够的，但是浸入这回事，与单纯将4维欧式空间中的3维流形与3维欧式空间做对应，还是有所不同的，不过它们是否能形成对应，我目前没有看到定理可以表明这件事情。
总结一下就是，我并不相信非欧几何渲染的存在，因为你无法改变看到的空间的欧几里得性，这时你会不会又要和我扯广义相对论，我也不知道怎么反驳，其实比起这个，我更相信非欧几何可视化这件事，确实有人做过这件事，详细可以看这个。而且在微分几何的道路上，还有好多需要学的东西，流形一个重要的部分就是局部欧式化，为什么欧式空间如此重要，其实我认为的实情是只有通过欧式空间才能认识这些非欧空间，因为计算怎么看都是来自欧式空间中的R，太复杂了，我永远也不会想明白的。
非欧几何渲染的可能性即是数字魔法。